


B.U.N.K. Volume 3, Number 1 (1986)
F.C. Thompson and D.R. Whitehead (1,2,3,4,5,6)
Systematic Entomology Laboratory IIBIII
Agricultural Research Service, USDA
c/o U.S. National Museum
Washington, D.C.
20560 U.S.A.
If systematic papers are to have a patina of scientific credibility, one or more games must be played. Cladistics is, de rigueur, a favored game. An elaborate cladogram (a sort of defoliated tree), however, betrays at best a mechanical tedium, and at worst, sheer ignorance. It requires ridiculous amounts of time to prepare, perhaps an artist's services, and space and money to publish.
What substitute will better serve to lend scientific credibility? Why, surely, what can be more elegant and eloquent than a "mathematical" formula? A simple cladistic hypothesis can be stated thus: Group X = Taxa (a+b)+(c+(d+e)). In plain English, a and b as well as d and e are sister groups, with group d+e being the sister of c and that group in turn being the sister of group a+b. ln the equation, the left hand element identifies the group being considered and the right, a cladistic formula, explains the relationships within that group. Even with names spelled out, relationships of a small number of taxa can be clearly expressed in but one or two printed lines. (9)
We restrict further discussion to end-point taxa in dichotomous models. Those who explore mathematical games (or gams, as that is what the typer tried to say (10)) may extend these ideas to more complex models. Cladistic formulae can be used to express any kind of branching relationships.
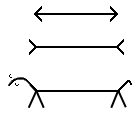
Our game is to explore perception. For our models to work (11), they must be dichotomous. Who would say that the following two lines are not identical, for instance?

Suppose, however, these lines are presented as: Wagnerian or Wagging networks? Which then is the longest? Or, by rules of parsimony (cheapskatedness), the shortest?
One fault of the standard cladogram is that its visual impact is linear, hence misleading. To overcome this each branching point or node should be considered as fully rotatable. Considered thusly, interesting numbers begin to emerge. For sets of 2, 3, 4, 5, and 6 end-point taxa, there are respectively; 1, 3, 15, 105, and 945 different sets of relationships regardless of rotatability of the nodes, and there are respectively; 2, 4, 8, 16, and 32 different ways to view each single cladogram when rotatability is considered (i.e. a different linear arrangement of the taxa or "isomorph"). Thus for the five-taxon example cited previously, there are 104 other possible hypotheses, and there are also 15 other ways to express the proposed hypothesis; in all, relationships among the five end-point taxa in a strictly dichotomous system may be expressed in 105 x 16 cladograms, or a total of 1680 visually different trees.(l2)
The formula given previously for Group X is one hypothesis, and it is one of 16 possible isomorphs. Per se, it has no advantage over a tree (except that it may not be botanical, so therefore it can apply to beetles). Lacking however, is the confusion of lines inherent in the tree; the hypothesis is reduced to symbolic logic, wherein elements shift mentally without recourse to repeated diagrams.
Our point is clear. Smash the optical illusion of linearity. Our reason should also be clear. Accommodate optically contradictory but compatible morphoclines. A few sample morphoclines will illustrate the point. In the formula: Group X = Taxa (a+b)+(c+(d+e)), relationships are indicated by morphoclines in characters 1, 2, and 3, thus:
 c
c  d
d 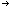 e
e
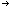 (d, e)
(d, e) 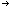 c
c
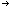 a
a 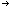 b
b
If the hypothesis is drawn directly as a tree, the illusion is that taxa a and e are least related, because they are on opposite sides of the tree. In the isomorphic formula: Group X Taxa (c + (d + e) ) + (a + b), rotatability is obvious; in the derivative tree, the illusion is that taxa a and e do not appear to be least related.
Whenever only a bare cladistic hypothesis is intended, the shorthand formula is the ultimate in elegance.
To summarize we ask two questions: (1), which network is longer?
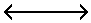 or
or 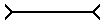
And, (2), which of the following trees are the same?

The answers are (1), neither, and (2), all. If you got both right, good: you are a true cladist, as reality means more than appearance. If you got both wrong, bad: you are a hopeless pheneticist, as appearances (overall similarity) are more important to you than reality. If you got one right, you are confused, uncertain as to whether reality or appearances are more important, hence belong to the eclectic school. And school is out!